A graphical model is a method for modeling probability distributions under certain uncertainty.

Toolbox:

  1. Representation: model uncertainty and encode domain knowledge
  2. Inference: answer questions \(P(X\mid m)\), where m is the model or data
  3. Learning: what model fits my data \(m = \operatorname*{argmax}_{m\in M} F(D,m)\).

Benefits:

  1. Efficient

    • (Expensive) The chain rule (aka product rule) allows to calculate joint probabilities.
    • (Cheaper) Using GM, we can model only those dependencies inferred by the graph, generating fewer parameters; encodes independence.

  2. Encode domain knowledge through priors and incorporate them in inference via Bayes theorem.

GMs vs PGMs:

  • GMs use multivariate function.

  • PGMs use multivariate distributions.

    Structure

    1. Edges represent relationship among the RVs.
    2. Directed nodes represent causality while undirected nodes represent correlation.

Bayesian Network and Markov Random Field

Bayesian Network

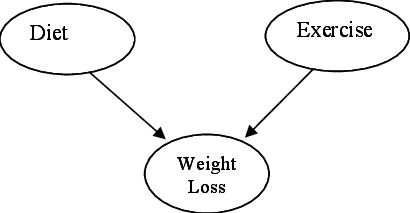
Bayesian Network

  • It is a directed acyclic graph (DAG) where each node has a Markov blanked (its parents, children and children’s parents).
  • A node is conditionally independent of the nodes outside its Markov Blanket.
  • Joint probability distribution is determined by the local conditional probabilities as well as the graph structure.
  • Model can be used to generate new data.

Markov Random Field

Markov Random Field

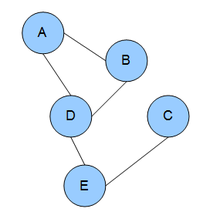
  • It is an undirected graph.
  • A node is conditionally independent of the other graph nodes, except for its immediate neighbors.
  • To determine the joint probability distribution, we need to know local contingency functions (potentials) as well as structural cliques.
  • This model cannot explicitly generate new data.