Topic Model Applications
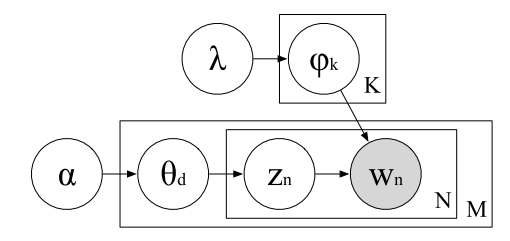
Topic Model
First attempts to find topics from data is Latent Semantic Analysis (LSA): find the best low-rank approximation of a document-term matrix. Approximation, based on SVD.
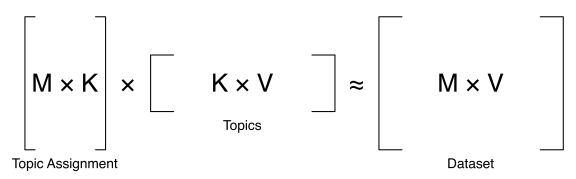
Latent Dirichlet Allocation
Latent because we use probabilistic inference to infer missing probabilistic pieces of the generative story.
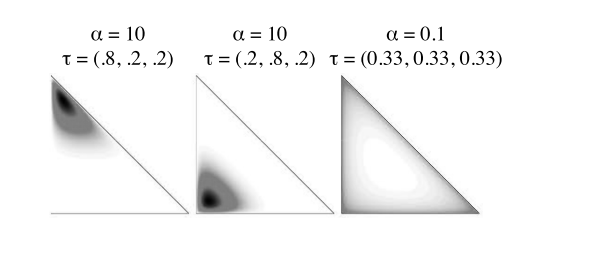
Dirichlet because of the Dirichlet parameters encoding sparsity. Allocation because the Dirichlet distribution encodes the prior for each document’s allocation over topics.
Story
- Generate Topics
- Document Allocations
- Words in Context
Inference (rvs.)
- Topic Assignments
-
Document Allocation
\[\theta_{d,i}\approx\frac{N_{d,i}+\alpha_i}{\sum_kN_{d,k}+\alpha_k}\] -
Topics
\[\phi_{i,v}\approx\frac{V_{i,v}+\beta_v}{\sum_wV_{i,w}+\beta_w}\] - Assign word to a particular topic
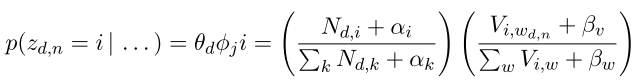
Information Retrieval
Ad-hoc IR
Where IR systems might look for the “needle in the haystack”, topic models will tell you about the overall proportion of hay and needles, and perhaps inform you about the mice that you did not know were there
Topic models helpful when we have a specific information need but no idea how to search for it
Traditionally: retrieve and rank documents by measuring the word overlap between queries and documents. Limited! Words with similar meaning or different forms should also be considered as matching keywords.
Language modeling: allows to capture semantic relationship
Query expansion: use background knowledge to interpret and understand queries and add missing words.
Document Language Modeling
Statistical language model estimates the probability of for word sequences
\[p(w_1,w_2,\dots,w_n)\]-
Often approximate using ngram models.
In a unigram model, words in the sequence are independent
\[p(w_1,w_2,\dots,w_n)=p(w_1)p(w_2)\dots p(w_n)\]Trigram assumes probability in a window of two words
\[p(w_1,w_2,\dots,w_n)=p(w_1)p(w_2\mid w_1)p(w_3\mid w_1,w_2)\dots p(w_n\mid w_{n-2},w_{n-1})\]
Then generate the probability of generating a given query (maximum likelihood)
\[p(q\mid d)=\prod_{w\in q}p(w\mid d)=\prod_{w\in q}\frac{n_{d,w}}{n_{d,.}}\]| For IR, rank documents based on p(q | d), but maximum-likelihood gives zero probability to unseen words and it can throw out good matches. Solve by allocating non-zero probability to missing terms, smoothing. |
Smoothing directions
-
interpolation: discount contribution of seen words and add contribution of unseen and seen words
Jelinek-Mercer: linear interpolation with the document and corpus using a coefficient, solving the data sparsity problem. Missing words falls back to the probability of the corpus level.
\[p(w\mid d)=(1-\lambda)p(w\mid d) + \lambda p(w\mid\mathcal{C})\] -
backoff: trust ML estimation for high count words and redistribute mass for less common words
Bayesian Smoothing using Dirichlet Priors: discrete distribution smoothed by applying Dirichlet priors with a concentration parameter.
\[p(w\mid d)=\frac{n_{d,w}+\beta p(w\mid\mathcal{C})}{\sum_{v\in V}n_{d,v} +\beta}\]
Applying Topic Models to Document Language Models
Lead relationship between query words and documents by marginalizing all topics.
\[p(w\mid d) = \sum_k p(w\mid k)p(k\mid d)\]- Combine Topic models and language models, see.
- Linear Interpolation + Jelinek-Mercer smoothing
- Linear Interpolation + Bayesian smoothing
Query Expansion in IR
Query-Word relationships for query expansion, two main steps:
-
Find relationships between queries and words and select top related words to expand query
\[\hat\theta_{Q'}=(1-\lambda)\hat\theta_{Q}+\lambda\hat\theta_{\mathcal{F}}\]Query language model: Combine query content with relevant documents (e.g. clicked documents). Find p(w q). Relevance Model: query and relevant documents are random samples from an unknown relevance model R
\[p(w\mid R)\approx p(w\mid q)=\frac{p(w,q)}{p(q)}=\frac{\sum_{d\in\mathcal{C}}p(d)p(w\mid d)p(q\mid d)}{p(q)}\] -
rank expanded queries and rank relevance scores
- Combine expanded query language model with query language model (see equation). Then compare topic distributions between query q generated and document d generated.
- Compute relevance score using original query and expanded query, the linearly combine the two scores, obtaining a final query-document relevance score.
Applying topic models for query expansion
Capture semantic relation between words by learning latent topics (distribution over words). Thus, it is a way to expand or match words at the semantic level.
-
Smoothing query language model: make query expansion and compute words relevance from topics directly.
\[p(w\mid q)=\sum_kp_{tm}(w\mid k)p_{tm}(k\mid q)\]However only queries are normally short and topic results are limited. A solution is to train topic models using the relevant documents (e.g. clicked documents)
-
Improving relevance model: improve the relevance model.
\[p(w\mid q)=\sum_{d\in\mathcal{C}}\left(\lambda p(w\mid d)+(1-\lambda)p_{tm}(w\mid d,q)\right)p(d\mid q)\\\text{,where }p_{tm}(w\mid d,q)=\sum_kp(w\mid k)p(k\mid d)p(q\mid k)\]Model captures word relationships on a semantic level: improves query-word relationships and query expansion.
-
Learning pair-wise word relationships: use topic models for query expansion by finding relationship between words and compute document rank scores.
\[p(w_x\mid w_y,\alpha)=\frac{\sum_kp(w_x\mid k,\alpha)p(w_y\mid k,\alpha)\alpha_k}{\sum_{k'}p(w_y\mid k',\alpha)\alpha_{k'}}\]Select top related terms as the expanded terms e for a given query q.
-
Interactive feedback: users feedback for the retrieval process and thus improving results. Show user a initial set of retrieval results and ask for feedback.
Beyond relevance - search personalization
-
Contextualization: consider user search activity (e.g. time, location, etc)
preference documents: concatenate clicked documents or top n ranked documents if no click happened
\[p(k\mid q)=\frac{p(k,q)}{\sum_kp(k,q)}\approx\frac{\text{sim}(\theta_k,\theta_q)}{\sum_k\text{sim}(\theta_k,\theta_q)}\]Then, rank preference documents using a query language model. First, infer latent topics p(w k) and then query-topics. However, queries q are often too short, so we could train a language model using the preference documents for query q and compare the cosine similarity against each topic k to estimate the query-topic distribution. -
Individualization: individual characteristics (users’ profile)
Given the topic distribution of the document, there will be words chosen at random to generate the query and users who chose to click that document (see paper).
\[p\left(k \mid w_{i}, d_{i}, u_{i}\right)=\frac{p\left(k, w_{i}, u_{i} \mid d_{i}\right)}{p\left(w_{i}, u_{i} \mid d_{i}\right)} \propto p\left(w_{i} \mid k\right) p\left(u_{i} \mid k\right) p\left(k \mid d_{i}\right)\]
Evaluation and Interpretation
Users need to understand a model’s output to draw conclusions. Understanding can be done by model visualization, interaction, and evaluation.
## Display Topics
Words with highest weight in a topic best explain what the topic is about.
- Word lists are a good way of showing topics, use lists, sets, tables, bars for word probability.
-
Word clouds use size of words to convey information.
Also, plot word clouds with word associations.
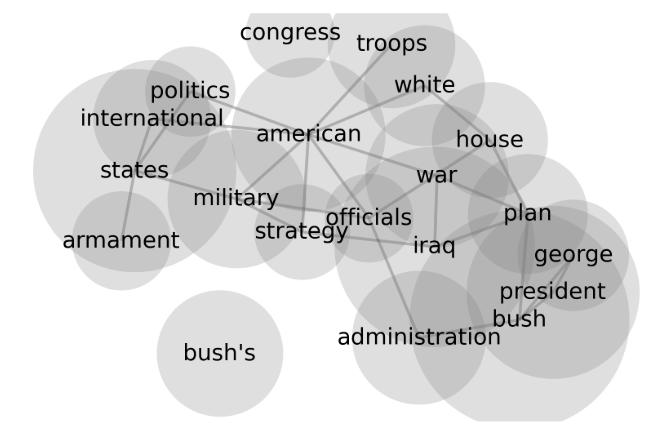
Labeling Topics
labeling focuses on showing not the original words of a topic but rather a clearer label more akin to what a human summary of the data would provide.
- Internal Information (unsupervised)
- Internal Labeling: take prominent phrases from the topic and compares how consistent the phrase context is with the topic distribution. It can be extended for hierarchies.
- External Knowledge (higher quality)
- Labelling with Supervised Labels: use human annotators to select a top word topic using a SVR (predict most representative word), paper.
- Labeling with Knowledge Bases: 1) align topic models with an external ontology; 2) build a graph, find matching words and rank them with page rank
- Using Labeled Documents:
- Labeled LDA provides consistent topics with the target variable.
- Labeled Pachinko Allocation for hierarchical label sets (e.g. labels: Ecuador → Country)
- Sup. Anchor: Use labels to compute anchor words, which are words that might define a topic.
Displaying models
- Find relevant documents: select a particular document-topic and sort them from largest to smallest.
- Plot how words are used within a topic
- How topics relate to each other?!
Evaluation, Stability and Repair
- Held-out likelihood of a model
- TM is a generative model: predict next unseen word
Find errors
- Documents with poor held-out likelihood are random noise
On the other hand, hundreds topics so specific that any held-out document is modeled well yields an excellent held-out likelihood.
- Held-out likelihood emphasizes complexity but interpretability
- Hyper-parameters play a important role
- Topic quality is a proxy to human interpretability but it doesn’t tell the parts where the model isn’t reliable or fails.
- Check if a dataset is good enough to apply topic modeling
a mismatch between the number of topics and documents, topics that are “too close together”, or a mismatch between the number of topics in a document and the Dirichlet parameter α.
Some projects
Future trends and other models
Guided LDA to seed topics with specific words or more recently CatE.
Dynamic Topic Model: each topic has a distinct distribution over words for each time period
cDTM: time is considered continuously
Author-Topic model: an author has a collection of topics that they write about and each document is a combination of the topics that its set of authors care about.
Inheritance topic model: adapt LDA to a citation network
Dynamic influence model: Find most influential documents
LinkLDA: relationship between documents
Short documents
- it can confuse topic modeling algorithms see these studies (see for a specific application in Twitter; also, interesting on how to apply and analyze topic models)
- to capture trends over time or across users, algorithms must know these connections between users or messages
- Topic model for sparse data or short texts
Supervised Topic model
Results vary based on the number of topics. The nested Dirichlet process provide a way of selecting the appropriate number of topics.
- Labelled LDA: it can do multi-class (see application on Twitter)
- Supervised LDA: sLDA for different response types
- MedLDA: changes objective function of sLDA that improve predictions (uses maximum margin similar to SVM to improve predictions)
Embedding Topic Model
- GATON: leverages the graph structure and word embeddings
- ETM: Learns a topic embedding and word embedding end-to-end
- DETM: Similar to ETM but considers time
Some notes
- Interesting application for reviews and sentiments
- Thematic variation is a hard problem in topic models since we expect that documents won’t change while reading (e.g.a novel)